数理最適化研究室
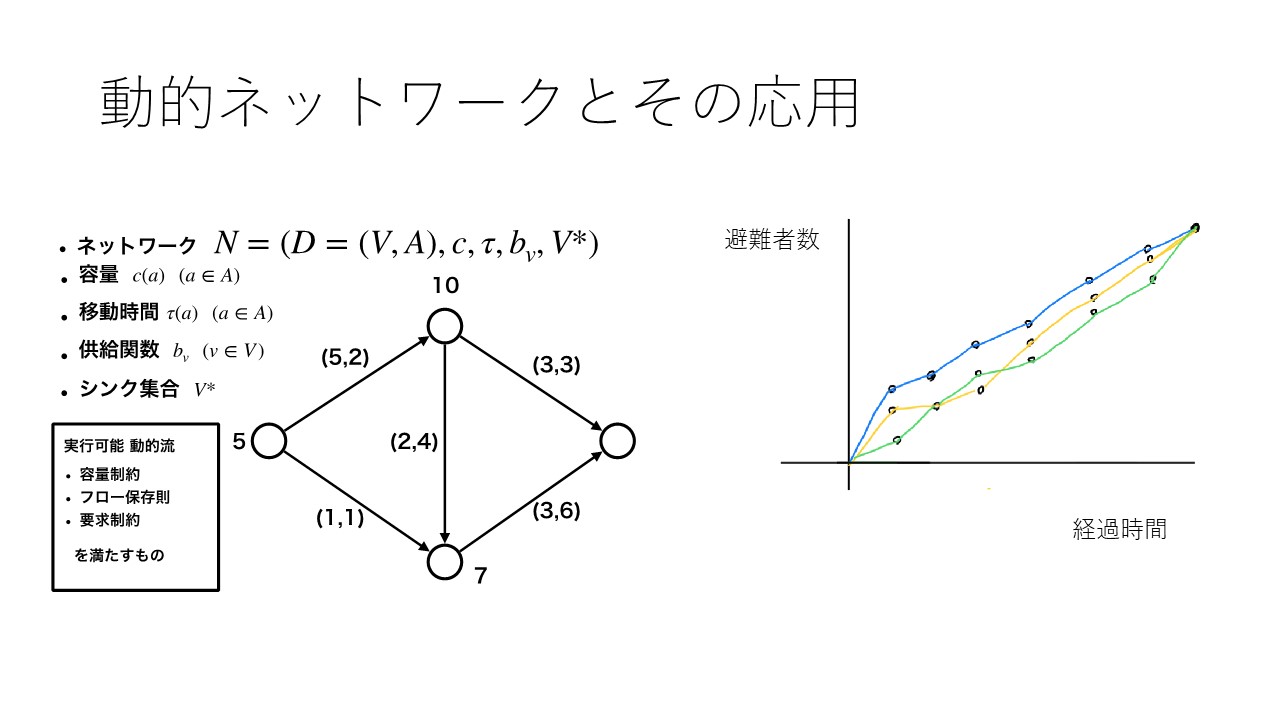
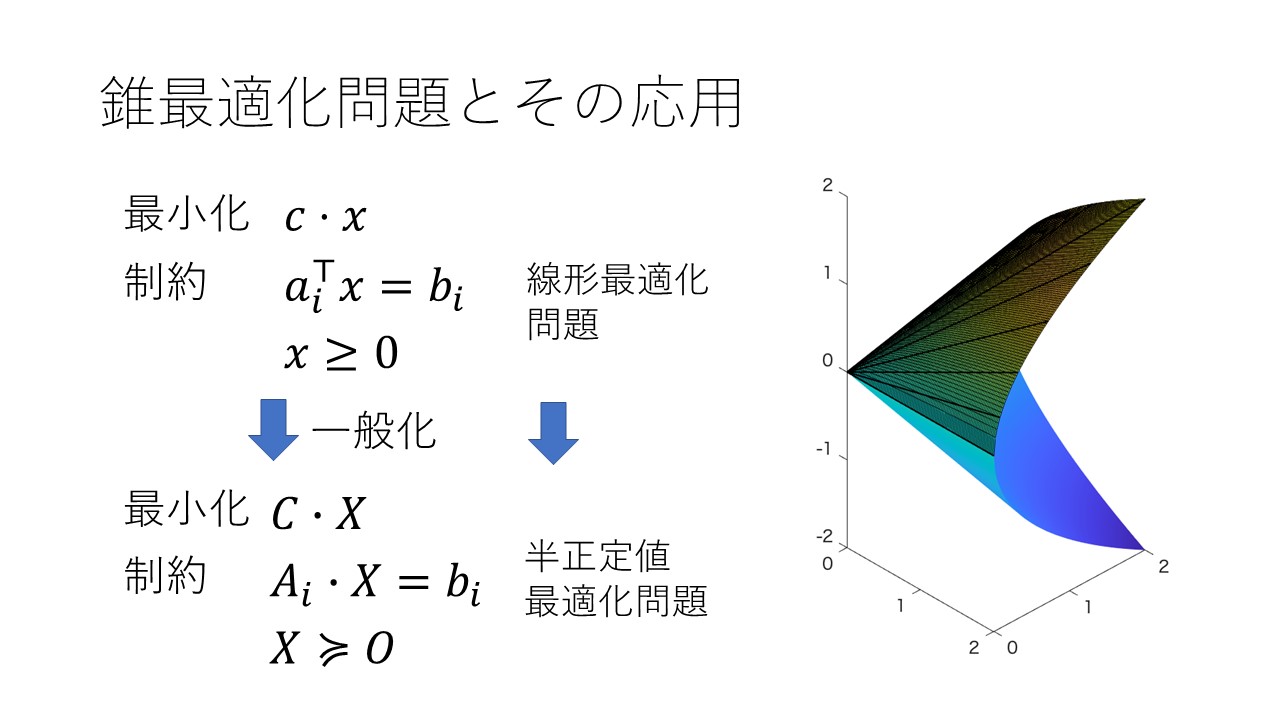
小林研究室の研究分野 数理工学の研究を行っています.数理最適化におけるアルゴリズムの開発と,そのコンピュータへの実装を行っています.また,今後発展の可能性のある新しい分野にも積極的に取り組んでいきます.数理最適化はその強力な問題解決能力から,ビジネスの様々な場面で活用されています.実務規模でその能力を発揮させるには,効率的なソフトウェアとして実装する必要があります.この研究室では,数理最適化の基盤理論から,実務規模データで動作するソフトウェア実装までを研究対象としています.具体的な研究テーマとして、(a)ロジスティクス工学、(b) 動的ネットワークとその応用、(c) 半正定値最適化問題とその応用、(d) 連続最適化の基盤的研究が挙げられます.
研究紹介
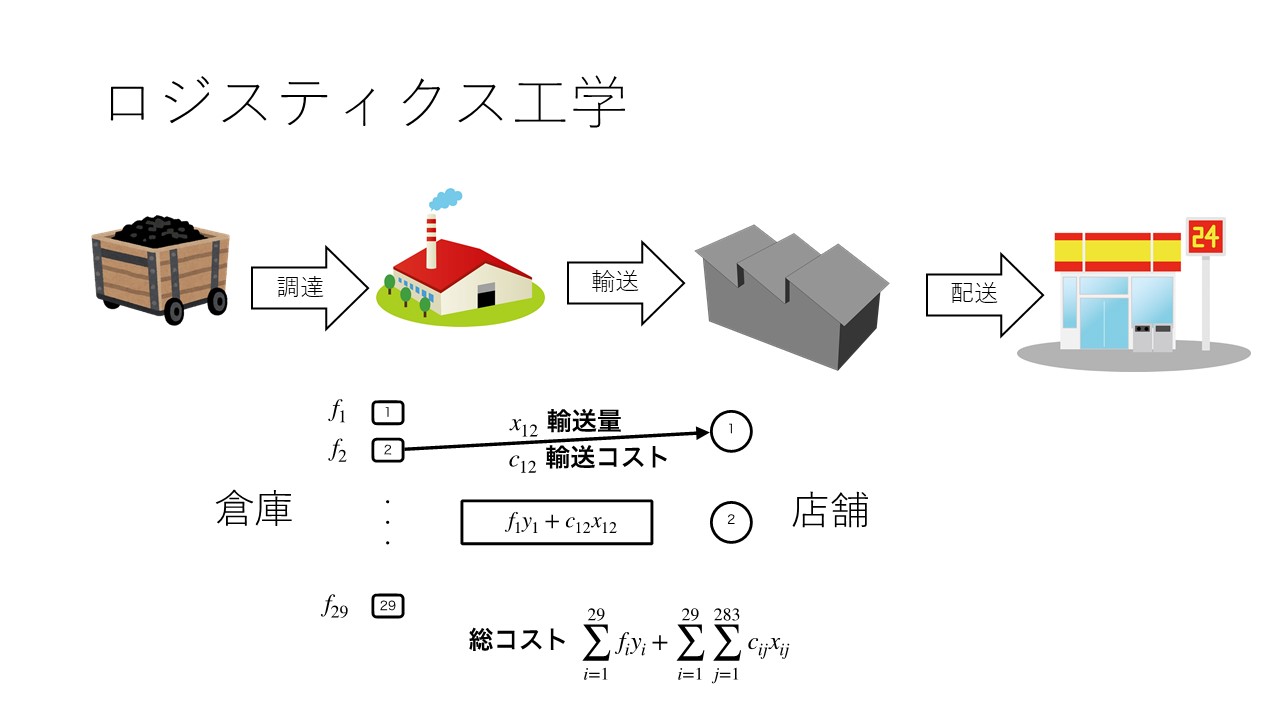
企業活動においては,施設配置,輸送計画,生産計画など,収益とコストに影響を与える計画・オペレーションがさまざま存在します.これらの活動に対して,数理最適化やシミュレーションの手法を用いてアプローチする分野を「ロジスティクス工学」と呼んでいます.この研究では,船舶スケジューリングや配送計画などロジスティクス工学で生じる最適化問題に対して,高性能なアルゴリズムの開発とソフトウェア開発を行います.さらに、開発したアルゴリズム・ソフトウェアを実験的に解析することで、その性能を評価します. 数理最適化は、様々な条件や目的を数式で表現し、目的を最小(または最大)にする計画を求める数理的手法のことを指します.線形最適化問題や最短路問題など,すでに様々な分野で用いられてきた実績のある方法と,理論的な成果によって最近実用になりつつある方法とを積極的に組み合わせることによって、新しい手法を生み出すことを目指しています.